Stand 14.05.2023

Reflexion der GPS-Signale an kleineren Objekten

Im Allgemeinen kann es an der jeweiligen Position der Empfangsantenne des GPS-Loggers für jeden Satelliten mehrere reflektierende Objekte geben.

Bild 1: Spiegelnde Reflexion Für dieses wie auch für alle weiteren Bilder: Für eine größere Darstellung     "Klick in das Bild""

Ebenso wird lediglich in Ausnahmefällen allein das Signal nur eines einzigen Satelliten von diesem Mehrwegeeffekt betroffen sein.
Im Fall einer (echten) Spiegelung würden davon nur jene wirksam werden, für die die Beziehung "Reflexionswinkel = Einfallswinkel" des Reflexionsgesetzes (Wikipedia) erfüllt ist, indem sich das Lot auf den reflektierenden Bereich ("dessen Normale") innerhalb der dem Satelliten, dem Reflexionspunkt und der Empfangsantenne gemeinsamen Ebene befindet (die "Einfallsebene" in nebenstehendem Bild 1), die ihrerseits – abhängig von der Position des Satelliten am Firmament – gegenüber dem Lot des Loggers auf die Horizontebene geneigt sein kann.

Als weitere Bedingung kann man ablesen:

"Das Einfallslot liegt in der Einfallsebene"

(≡ "Die Einfallsebene steht im rechten Winkel zur Reflexionsebene").

Ebene Welle am kleineren Objekt

In einem Gedankenexperiment sei davon ausgegangen, dass die Signalübertragung vom Satellit zur Empfangsantenne in der Art von Bild 3 in einem einzelnen Strahl erfolgt, dessen Verlauf gleich dem der Sichtlinie "einschließlich deren Spiegelung an der Reflexionsebene" ist. Bewegen der Antenne oder des Satelliten hat ein Wandern des Reflexionspunkts in der Reflexionsebene zur Folge. Solange er sich innerhalb der Berandung des – bei diesem Gedankenexperiment ausreichend groß angenommenen – reflektierenden Objekts befindet, kommt ein spiegelnder Empfang hoher Intensität zustande. Überschreitet der Reflexionspunkt die Berandung nach außen, kann die Winkelbeziehung des Reflexionsgesetzes nicht mehr eingehalten werden – die Empfangsantenne wird nicht mehr vom gespiegelten Strahl erreicht. Dann dürfte der Empfangs-Pegelverlauf längs des Weges des Reflexionspunkts im Bereich des Randes des spiegelnden Objekts dem durch das Phänomen der Beugung bestimmten Pegelverlauf ähneln, der sich an einer (echten, freistehenden) Kante beim Übergang in den abgeschatteten Bereich abhängig von deren Überstand über der ununterbrochen – durch das Hindernis hindurch – verlaufend gedachten Sichtlinie ergibt.

In Wahrheit gelangt das Satelliten-Signal als eine (aufgrund der sehr großen Entfernung) ebene Wellenfront an das Objekt. Ihr entspricht im nachfolgenden Schnittbild (Bild 2) das in Weiß gehaltene Bündel paralleler Strahlen, dem eine (vertikal zur Bildebene sehr lang ausgedehnte) dünne Platte (schwarz) entgegengestellt ist. Als von ihr ausgehend kann man sich auch hier die im Eintrag "Mechanismen der Weitergabe der GPS-Signale über Objekte der Umgebung" aufgezählten drei Komponenten vorstellen:

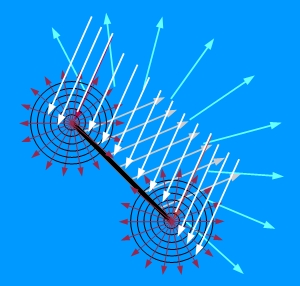Bild 2: Signalweitergabe an einer dünnen Platte

• eine durch Spiegelung entstehende Komponente in Gestalt eines dem Umriss des Objekts entsprechend räumlich begrenzten Ausschnitts aus der Wellenfront – hellgraues Bündel paralleler Strahlen,
• eine ungerichtete Komponente, die von der diffusen Reflexion an den Unebenheiten des Objekts herrührt – die hellblauen Strahlen (Genaueres zur u. a. aus der Oberflächenbeschaffenheit resultierenden Richtungsabhängigkeit siehe z. B. [Keydel 2010] Seite 11),
• Komponenten (rote Strahlen) in Gestalt der Zylinderwellen, die an der Berandung des spiegelnden Objekts von den rot dargestellten Strahlen des Bündels parallel einfallender Strahlen verursacht werden (vergleiche GPS-Ecke: Kanten-Beugung; allgemein: Stichwort "Knife-Edge") .

Aufgrund der vorausgesetzten Längsausdehnung des reflektierenden Objekts werden die von den Kanten ausgehenden Signalbeiträge als Zylinderwellen weitergegeben. Mit den grünen Pfeilen in Bild 2 soll angedeutet werden, dass diese Beiträge in "ausreichend" großem Abstand von der Platte zusammen mit dem infolge von Oberflächenrauigkeit der Platte entstehenden Beitrag zu einer einzigen Zylinderwelle mit einer von der Richtung innerhalb der Papierebene abhängigen Intensität verschmolzen erscheinen (Stichworte "Interferenz", "konstruktive und destruktive Überlagerungen"). Solange es abhängig von der Orientierung von Satellit, Empfangsantenne und Platte zu einer Reflexion an der Platte kommt ("es gibt dort einen Reflexionspunkt") tritt zu diesem Signalgemisch der dann zumeist dominierende Beitrag aus der Spiegelung als ebene Welle hinzu.

Die Kontur des am kleinen Objekt reflektierten Strahlenbündels entspricht unter Berücksichtigung des für den Ort der Empfangsantenne zutreffenden Einfalls- bzw. Ausfallswinkels α des Satellitensignals der Kontur des Objektes (α gemessen zwischen LOS und Einfallslot – vergleiche Bild 3); sie erscheint somit gegenüber der Originalkontur um den Faktor cos α parallel zur Einfallsebene gestaucht.

In den Bereichen der Abschattungsgrenzen der einzelnen Kanten der Platte sind die für die "scharfe Kante" beschriebenen Effekte zu erwarten, in – verglichen mit dem Abstand der Kanten – größerer Entfernung: richtungsabhängig regelmäßige Interferenzmuster aus Überlagerungseffekten der Komponenten der beiden Kanten-– verwandt mit dem Interferenzmuster an einem Spalt mit der Breite der Platte. Verringern der Kantenabstände auf Bruchteile einer Wellenlänge lässt schließlich auch diese Interferenzmuster verschwinden – gleichbedeutend mit einer von Hindernissen dieser Art ausgehenden Zylinderwelle mit von der Richtung unabhängiger Intensität.

Die Berandungen realer Objekte gehorchen kaum einfachen geometrischen Beziehungen. Dann dürfte es zu regelloser kleinräumiger (bezogen auf das Objekt) Richtungsabhängigkeit bzw. (allgemeiner) Ortsabhängigkeit des Empfangspegels kommen. Beim Verringern der Erstreckung des Objekts in alle Richtungen auf Bruchteile einer Wellenlänge werden dann jegliche kleinräumigen Änderungen der Intensität des weitergegebenen Signals verschwinden, gleichbedeutend mit dem Übergang zur Gestalt einer vom Objekt ausgehenden Kugelwelle.

Gegebenheiten des Zustandekommens von Umwegen

Umwege bei Spiegelung

Das untenstehende Bild 3 soll den Blick auf eine parallel zur Horizontebene zu denkende Ebene darstellen – mit 4 reflektierenden Objekten (1 bis 4) –, in deren Punkt E sich die Antenne eines GPS-Empfängers befindet. LOS bezeichnet die Sichtlinie von E zu einem ("unendlich") weit entfernten, in der gleichen Ebene gelegenen GPS-Satelliten.

Die vier Objekte stellen je ein kleineres Objekt, für einzelne Betrachtungen auch einen Ausschnitt aus einer längeren Wand, dar. Bei den folgenden Betrachtungen sei angenommen, dass allein das jeweils untersuchte Objekt existiert. Gegenseitige Abschattungen der Objekte sind somit nicht zu berücksichtigen.

Die Strahlen I bis III liegen gemeinsam mit der Antenne ebenfalls in der horizontalen Ebene. Sie markieren, wie alle weiteren, beliebig eng verlaufenden, hier nicht dargestellten Strahlen, jeweils einen Signalweg vom Satellit zur Antenne. Ihr Verlauf wird aufgrund der (verglichen mit den in der Ebene quer zur Sichtlinie gemessenen Ausdehnungen viel größeren) Satellitenentfernungen als parallel zur Sichtlinie angenommen ("Parallelstrahlen").

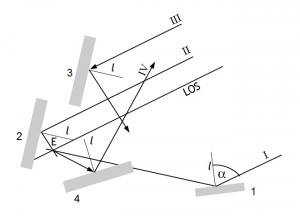Bild 3: Spiegelung an (unendlich großen) Objekten

Indem die Wände und die Ebene mit der Antenne im rechten Winkel zueinanderstehen, ist die erste Bedingung dafür erfüllt, dass die mit l bezeichneten Linien, die ebenfalls zur Ebene von E gehören, Einfallslote für die Strahlen I bis IV sein können. Ihre Aufsetzpunkte an den Wänden markieren somit jeweils einen Reflexionspunkt, für den der Weg des reflektierten Satelliten-Signals betrachtet werden soll.

Die beiden Möglichkeiten des Vorgehens der Suche nach diesem Weg sind an den Objekten 3 und 4 gezeigt. Im Fall von Objekt 3 mit dem Strahl III wird der Weg von der Einfallsrichtung des Satellitensignals aus verfolgt. Es ist ersichtlich, dass das reflektierte Signal den Empfänger nicht erreichen kann sondern ihn weit verfehlt. Der Ausbreitungsweg über den Reflexionspunkt am Objekt 4 wird in der entgegengesetzten Richtung verfolgt (als würde mit der Empfangsantenne gesendet): Anders als bei den Objekten 1 und 2 mit den Strahlen I und II verfehlt der Strahl IV das Ziel, den Satellit.

An dieser Stelle erhebt sich die Frage, ob es an den sich dazu über die dargestellten Rechtecke hinaus erstreckend angenommenen Objekten 3 bzw. 4 dennoch Reflexionspunkte geben könnte, über die eine Verbindung zum Punkt E möglich ist. Der Verlauf der Strahlen I, II und III parallel zur Sichtlinie und zueinander (Stichworte: Satellit in unendlich großer Entfernung; Wellenfront eben), die sich alle an einem Punkt, E, treffen sollen, verweist auf zum Sender geöffnete Parabeln, die so angeordnet sind, dass sich ihre Symmetrieachsen mit der Sichtlinie und die Brennpunkte mit dem Punkt E decken.

Eine Schar von Parabeln dieser Art mit der Sichtlinie als Symmetrieachse wird ebenfalls durch Gl.(3) aus der Herleitung zur Kantenbeugung^Anm1 beschrieben:

mit

d = auf der Sichtlinie gemessener Abstand vom
Brennpunkt E mit dem Empfänger,

h = senkrechter Abstand eines Parabelpunktes von der Sichtlinie,

λ = Wellenlänge des GPS-Signals,

ν = die Parabel charakterisierender Parameter
– mit ν = u / (λ/2) als Vielfachem einer halben
Wellenlänge (u ist der zugehörige Umweg), eine
reelle positive Zahl (jede Parabel hat zwei Äste)

Herleitungen wie der zur obigen Formel für h liegt zugrunde, dass (im Einklang mit der dazu vorausgesetzten Parallel-Strahlen-Eigenschaft) die Entfernung des Senders ein großes Vielfaches der Abstände der betrachteten reflektierenden Objekte vom Empfänger ist. Bei jeder dieser Parabeln handelt es sich um den in der engeren Umgebung eines der Brennpunkte – hier des Brennpunkts mit dem Empfänger – gelegenen parabelförmigen Teil einer Ellipse mit für alle Punkte gleicher Länge des Weges zwischen den Brennpunkten, den Orten von Sender und Empfänger, somit um eine Linie gleicher Umweglänge u aller ihrer Punkte.

Für diese Umweg-Linien gilt bekanntlich, dass der Wert u des für die gefundene Position bedeutsamen Umwegs als das Zweifache des Abstandes des bei d_o gelegenen Scheitels vom Brennpunkt abgelesen werden kann.

Dem entspricht in obiger Formel h = 0, wofür man mit den hier vorliegenden Umweg-Parabeln wie auch mit den eigentlichen Umweg-Ellipsen erhält:

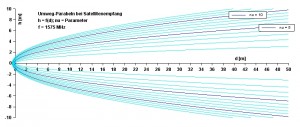Bild 4: Empfängernaher Ausschnitt aus einigen Umweg-Ellipsen – In der Nähe des Satelliten- empfängers nehmen die Umweglinien die Gestalt von Parabeln anAnm3

d₀ = – ν·λ/4.

Parabel-"Schar" aus beliebig vielen, beliebig eng benachbarten Linien: ν ist eine (positive) reelle Zahl. Das nebenstehende Bild 4 zeigt mit einigen ganzzahligen Werten lediglich eine kleine Auswahl solcher ν-Parabeln^Anm2.

Als Teil einer sehr weiträumigen Ellipse erstreckt sich jede Parabel durch alle vier Quadranten des dargestellten d,h-Koordinatensystems.

Ein gleichartiges Bild gilt auch für die Umgebung einer Sendeantenne – allerdings sind dort im Fall des Satellitensenders aufgrund seiner Auslegung keine Objekte zu erwarten, die als Reflektor wirken könnten (Reflexionen an Bauteilen des Satelliten können – aufgrund von Maßnahmen zu deren Vermeidung seitens der Konstruktion und nicht zuletzt wegen der im Interesse eines hohen Antennengewinns zugleich auch stark bündelnd wirkenden Sendeantennen – vernachlässigt bleiben).

In der Umgebung des Empfängers spiegelnd reflektierte Parallelstrahlen werden dann dessen Antenne treffen, wenn es in der Parabelschar diese Reflexionsebenen tangierende ν-Parabeln gibt^Anm4.

Im nachfolgenden Bild 5 (zur Verdeutlichung jedoch anders als im Bild 4 bei etwas überhöhten Achsenmaßstäben) wird das für die vier Objekte von Bild 3 untersucht. Dort ist das Objekt 1 (Strahl I parallel zur LOS-Linie) zu sehen, das die Parabel ν₂ tangiert; ähnlich auch beim Objekt 2 (Strahl II) mit der Parabel ν₁.

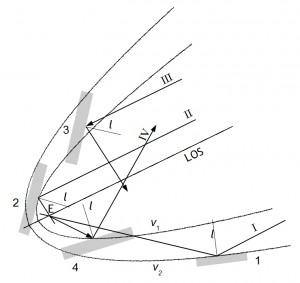Bild 5: Reflektierende Objekte, zwei davon mit   tangierenden Parabeln

Im Fall des Objekts 3 liegt der Schnittpunkt der Sichtlinie mit der – in Gedanken erweiterten – Reflexionsebene vom Sender aus gesehen vor dem Brennpunkt, so dass eine Reflexion zum Empfänger nicht zustandekommen kann. Auch jeglicher andere reflektierte Parallelstrahl kann den Empfänger nicht erreichen, denn die beliebig erweiterte Ebene von Objekt 3 liegt vom Sender aus gesehen vor dem Empfänger, würde ihn verdecken. Beim für das Objekt 4 willkürlich angenommenen Reflexionspunkt würde ein Parallelstrahl die Sichtlinie erst hinter E schneiden. Hiermit steht der für diesen Reflexionspunkt eingetragene Verlauf des in Gegenrichtung^Anm5, d. h. vom Empfänger ausgehend angenommenen Strahls – Teststrahl IV – in Einklang: An diesem Punkt trifft er viel zu steil auf die Reflexionsebene. Wegen deren geringer Neigung gegenüber der Sichtlinie würde der Reflexionspunkt für die Reflexion eines Parallelstrahls in den Punkt E (an einer etwas schlankeren Parabel, mit entsprechend kleinerem ν) weiter rechts, bereits außerhalb des dargestellten Bereichs, liegen.

Zum obigen Bild 5 wurde eine Satellitenposition in der Horizontebene vorausgesetzt. Im allgemeinen Fall eines höherstehenden Satelliten wäre die gesamte zu E gehörende Ebene mit der als LOS, Sichtlinie, bezeichneten Geraden (zusammen mit der gesamten Parabelschar und allen Parallelstrahl-Verläufen) durch Ankippen auf diesen auszurichten. Drehachse ist dabei eine in der Horizontebene liegende Linie durch E, die rechtwinklig zur Sichtlinie verläuft.

Eine der dabei eintretenden Folgen ist, dass die rechtwinklige Orientierung zwischen der Ebene im Bild 5 und den Wänden (entlang der Schnittlinie beider Ebenen) – eine der Voraussetzungen dafür, dass ein reflektiertes Signal die Antenne erreichen kann – für die neue Lage der Ebene verloren geht^Anm6. Das Wiederherstellen dieser Bedingung bedeutet, die Ebene zusätzlich, abhängig von der Satelliten-Elevation, um die Sichtlinie zu rotieren, bis unter Bewegung der Schnittlinie näher zur Horizontebene der rechte Winkel zur Objektebene erreicht ist. Auf dieser Schnittlinie befindet sich dann, falls diese aufgrund der geometrischen Gegebenheiten zustandekommt, der neue Reflexionspunkt – im allgemeinen bei einer anderen Umwegparabel, also veränderter Länge des Umwegs. Ähnliches wäre von vornherein im Fall von Objekten erforderlich, deren Reflexionsebene nicht rechtwinklig zum Boden orientiert ist. Zum Erfassen von z. B. Reflexionen an horizontalen Flächen (z. B. dem Erdboden) müsste stets ein Rotieren der Ebene mit der (zweidimensionalen) Parabelschar um bis zu 90° erfolgen.

Verallgemeinerung:

• Im Fall über dem Horizont befindlicher Satelliten tritt an die Stelle der zweidimensionalen Situation von Bild 5 eine räumliche.
• Der dreidimensionalen Situation wird das Erweitern der tangierenden Parabeln zu die Reflexionspunkte tangierenden Rotations-Paraboloiden mit der Sichtlinie als Achse gerecht (aus der "Suche nach der tangierenden Parabel" wird die "Suche nach dem tangierenden Rotationsellipsoid").

Bild 6: Umwegparabeln – Umwege u im 1-Meter-Raster   Empfänger bei (0,0) (Download der Bilddatei im PDF-Format)

Die Darstellung auf Basis des auf die Wellenlänge bezogenen Parameters ν (wie z. B. im Bild 4) bedeutet, dass sich die Verläufe mit Änderung der Wellenlänge bzw. Signalfrequenz verlagern würden. Im Fall der festen Signalfrequenz des GPS-Signals erleichtern sie Betrachtungen, bei denen Phasenbeziehungen eine Rolle spielen (wie z. B. bei Interferenz-Erscheinungen). Anders vermitteln die Verläufe im Bild 6 direkt geometrische Bezüge, wichtig z. B. zur Beurteilung von durch Objekte der Umgebung verursachten Fehlern der gefundenen Position (Vergleich mit Bild 4: u = 1 m entspricht etwa 5 λ, somit ν = 10).

An den Bildern 4 und 6 für den Fall der spiegelnden Reflexion abzulesen

– Objekte in der "Halbebene vor dem Empfänger" ("vom Sender aus gesehen": Objekte, die näher am Sender gelegen sind als die Empfangsantenne; d ≥ 0):

• Je weiter ein Objekt von der Empfangsantenne entfernt ist, desto flacher verläuft der zugehörige Signalweg gegenüber der Objektebene bei zugleich kleinerer für die Signalweitergabe wirksamer Fläche, die

  proportional dem Sinus des Erhebungswinkels der Umweglinie über der Objektebene ist,

  bzw. proportional dem Sinus des halben Erhebungswinkels des Objekts gegenüber der Sichtlinie,

  somit also (vergleiche oben) um so kleiner wird, je flacher der Signalweg verläuft.

• Bei gleichbleibender Ablage h eines (reflektierenden bzw. auch streuenden) Objekts gegenüber der Sichtlinie ist der zugehörige Umweg u umso kleiner gegenüber h (maximal gleich h), je weiter das Objekt von der Empfangsantenne entfernt ist.

– Objekte in der "Halbebene hinter dem Empfänger" (d ≤ 0):

• Je weiter ein Objekt bei gleichbleibender Ablage h gegenüber der Sichtlinie von der Empfangsantenne entfernt ist, desto steiler verläuft der zugehörige Signalweg gegenüber der Objektebene (entsprechend größer ist deren Neigung gegenüber der Sichtlinie, zwischen 45 und 90 °) bei zugleich größerer Annäherung der für die Signalweitergabe wirksamen Fläche an die Fläche des Objekts.
• Bei gleichbleibender Ablage h des Objekts gegenüber der Sichtlinie ist der zugehörige Umweg u umso größer (h ≤ u ≤ 2⋅|d|), je weiter das Objekt von der Empfangsantenne entfernt ist.

An Objekten hinter sowie seitlich des GPS-Empfängers gespiegelte Signale können somit mit besonders hohen Verzögerungen behaftet sein^Anm7.

Umwege bei diffuser Reflexion, Beugung – "Streuung"

Falls aufgrund der Orientierung von Satellit, kleinem Objekt und Empfangsantenne eine spiegelnde Reflexion nicht zustande kommen kann, verbleiben als dennoch und von der Orientierung der Objekte unabhängig vorhandene Mechanismen der Signalweitergabe

die diffuse Reflexion – an den Rauigkeiten des Objekts – vgl. "Gerichtete und diffuse Reflexion von GPS-Signalen" (GPS-Ecke)

und

die Beugung – an den Konturen des Objekts – dabei allerdings, aufgrund der geometrischen Gegebenheiten, überwiegend mit kleineren Ablenkwinkeln bzw. Umwegen als bei der "Beugung der GPS-Signale an Kanten abschattender Hindernisse" (GPS-Ecke) betrachtet,

allgemeiner – für beide gemeinsam, oft auch gemeinsam mit der Weitergabe durch Spiegelung –: In der Gestalt von Streuung. Weitergabe infolge Streuung bedeutet die Signalweitergabe weit über Pfade, die allein der Spiegelung gemäß der tangentialen Ausrichtung an Umwegparabeln entsprechen, hinaus, somit eine erhebliche Zunahme der Anzahl von mögliche Umwegpfade verursachenden Objekten gegenüber dem Fall allein der Spiegelung.

Die entstehenden Umwege ergeben sich auch hier einzig aus der räumlichen Zuordnung von Satellit, streuendem Objekt und Empfangsantenne. Zur Veranschaulichung eignen sich ebenfalls die Umweg-Rotations-Paraboloide.

Spiegelndes Objekt und Öffnung: Ausbreitungsverhalten

Zunächst sei daran erinnert, dass man im Fall der Signalweitergabe über ein spiegelndes Objekt zur Untersuchung des Strahlengangs zwischen einem Sender und einem Empfänger so vorgehen kann, dass man den dabei reflektierten Bereich an der Reflexionsebene als Symmetrieebene spiegelt – bei z. B. der Betrachtung aus der Richtung des Empfängers also den Sender. Dabei wird aus der infolge der Reflexion am Objekt zu einer Umweglinie umgebrochenen Sichtlinie eine durchgehend geradlinig verlaufende virtuelle Sichtlinie vom virtuellen Sender (eigentlich seinem virtuellen Bild) zum Empfänger, und der Strahlengang am Spiegel unterscheidet sich nicht vom Strahlengang durch eine mit dem Spiegel deckungsgleiche Öffnung in einer lichtundurchlässigen Ebene.

Unter Außerachtlassung von material- und polarisationsabhängigen Pegelverlusten gibt es – unter ansonsten gleichen geometrischen Gegebenheiten (Konturen und Orientierung im Raum stimmen überein) – Ähnlichkeiten,

Gemeinsamkeiten, aber auch Unterschiede

des Ausbreitungsverhaltens auf dem Weg über ein spiegelndes Objekt, also entlang einer Umweg-Linie, mit dem Ausbreitungsverhalten entlang der Sichtlinie durch die gedachte Öffnung hindurch.

• Gemeinsamkeiten der gedachten kleinen Öffnung mit dem
  kleinen spiegelnden Objekt:

  Bei feststehend angenommenen Ebenen erreicht der Signalweg
  sowohl
  durch die gedachte Öffnung hindurch als auch über das spiegelnde Objekt
  nur einen kleinen Raumwinkel des Bereichs hinter der Öffnung bzw. des am Objekt gespiegelten Bereichs. Die Lage dieses Raumwinkels ergibt sich aus der Position der Öffnung bzw. im Fall des spiegelnden Objekts zusätzlich aus dessen Orientierung, sein Betrag aus der wirksamen Fläche, die bei beiden umso kleiner wird je flacher der Signalweg gegenüber der jeweiligen Ebene verläuft.

  Vgl. [Gross 2003], S. 231, oder auch Eintrag in Wikipedia.de – Babinet’sches Prinzip^Anm8: Wenn mit dem Empfänger als Bezugspunkt die Geometrie der Berandungen beiderlei Objekte übereinstimmt, ergibt sich (ggf. bis auf eine Ausnahme im Zentrum) aus der Beschaffenheit der Beugungsmuster: Die Intensitäten der gebeugten Signale an der Empfangsantenne sind in beiden Fällen gleich, die Phasenlagen (hier kaum von Bedeutung) um π verschieden.

• Unterschiede des spiegelnden Objekts gegenüber der
  gedachten Öffnung:

  Bei festgehaltenem Reflexionspunkt kann die
    Reflexionsebene eines spiegelnden Objekts prinzipiell beliebig im Raum geneigt
  sein, so dass die Richtungen ihres Einfallslots, bei denen ein reflektiertes Satellitensignal die Empfangsantenne erreichen kann, den gesamten hinter dem Empfänger befindlichen Halbraum abdecken können, die Einfallsrichtungen, aus denen Satellitensignale den Empfänger erreichen können, sogar den vollen Raumwinkel Ω = 4 π.

  (Praktische Bedeutung: Durch Spiegelung werden an den Empfänger sowohl direkt vom Satelliten stammende als auch bereits am Erdboden oder an Hindernissen reflektierte Satellitensignale weitergegeben.)

  Bei festgehaltener Öffnung ergibt sich die Einfallsrichtung allein aus deren Position im Halbraum, unabhängig von der Orientierung der Öffnung im Raum.

Die Signalweitergabe durch eine Öffnung ist wohl besonders für Innenräume von Bedeutung: Ein direkt durch eine Öffnung in einen Innenraum gelangendes Satellitensignal trifft nur selten die Empfangsantenne, sondern sein Auftreffpunkt wandert entlang von Innenwänden und Boden, wo er erstmals, und nachfolgend von dort aus im Rauminneren noch viele Male, reflektiert wird, um allerdings mit den infolge Transmission durch die Außenwände dringenden Signalbeiträgen zu konkurrieren^Anm9 – zu Transmissionsdämpfungen in Wänden siehe z. B. [Michler,Strey 1998], [Strang ua 2008] – Tabelle 7 (Seiten 35 bis 36).

Auswirkungen von Ortsveränderungen auf Mehrwegesignale

Für alle beim GPS-Empfang beteiligten Objekte kann zutreffen, dass sie sich in Bewegung befinden –

im dem Einsatzzweck entsprechenden mobilen Betrieb

• für den GPS-Logger bzw. den Empfänger in GPS-Geräten,

stets

• für die GPS-Satelliten,

sowie nicht selten auch

• für das räumlich begrenzte Objekt.

Im allgemeinen wird es so dazu kommen, dass das Signal eines bestimmten Satelliten über ein räumlich begrenztes Objekt abhängig von der Zeit aufgrund des sich verändernden Einfallswinkels am Objekt zunächst diffus gestreut, sodann spiegelnd und schließlich wieder diffus gestreut weitergegeben wird^Anm10. Die Auswirkung ist eine meist beträchtliche Abhängigkeit des Pegels des Umwegsignals an der GPS-Antenne vom jeweils wirksamen Übertragungsmechanismus und der für diesen zutrefffenden Materialeigenschaft des Objekts. Während die Länge des Umwegs allein durch die Änderungen der Geometrie bei den Bewegungen bestimmt wird, werden sich den zum Umweg gehörenden Phasenänderungen noch am Objekt selbst entstehende Phasenänderungen als Folge vom Einfallswinkel abhängiger Materialeigenschaften des Objekts überlagern.

Auch wenn es sich "nur" um Resultate handelt, die mit einem Modell gewonnen wurden, das jedoch auf Messwerten aus der Galileo-Messkampagne 2002 des Deutschen Zentrums für Luft- und Raumfahrt (DLR) in einer urbanen Umgebung beruht, verdeutlichen die Bilder 18 bzw 20 in [Lehner u.a. 2009] zum einen die Vielzahl reflektierender Objekte, zum anderen aber die selbst beim Tempo eines Fußgängers zumeist nur kleinen Verweilzeiten eines GPS-Empfängers in den reflektierten Strahlenbündeln. Bei der Messwertgewinnung in GPS-Loggern sind oft Zeitabstände gleich 1 s (bei einer Signalerfassungszeit jeweils gleich 1 ms) üblich – mit somit bereits erheblich voneinander verschiedenen Empfangssituationen;zur Größenvorstellung: Der Abstand der horizontalen Gitterlinien in den oben genannten Bildern 18 bzw. 20 entspricht mit 0,1 μs Umwegunterschieden von 30 m.

Anmerkungen

^Anm1  Der Strahlengang bei Reflexion stimmt mit dem Strahlengang im Bild 1 eines Satellitensignals an einer scharfen Kante überein, wenn man sich an der Stelle der Kante den Reflexionspunkt eines spiegelnden Objekts denkt, das so ausgerichtet ist, dass das reflektierte Signal den Empfänger trifft.

^Anm2  Betrachtungen mit Verwendung des Parameters ν, ebenfalls als ν = u / (λ/2) definiert, sind auch in der Theorie der Funkübertragungstechnik gebräuchlich – wie ab etwa 1950 bei der zunächst mit Analogsignalen betriebenen Richtfunktechnik, aber auch beim Satelliten-TV-Empfang – beide verwenden stärker bündelnde Antennen (Empfängerseitig erübrigen sie sich dagegen bei den GPS-Anwendungen wegen der prinzipbedingt notwendigen Weitwinkel-Charakteristik der Empfangsantenne).

Allerdings spielen dabei nur ganzzahlige positive Werte von ν eine Rolle – als Nummern von Fresnel-Zonen.

"Nummer der Fresnelzone", "Umweg-Ellipsoid", "ν-Parabel" … : Grund des in der deutschsprachigen Literatur bevorzugten Sprachgebrauchs mit der “Nummer der Fresnel-Zone” könnte das Anliegen der Unterscheidung gegenüber dem eigentlich naheliegenden, aber längst in der Optik vergebenen Begriff "Fresnel-Zahl" sein – vergl. z. B. den Artikel zur Fresnel-Zahl in Wikipedia.de; ähnlich gibt es auch "Fresnel-Ellipsoid" (besonders in Veröffentlichungen in Englisch für den Bereich der 1. Fresnel-Zone verwendet) eigentlich schon längst im Zusammenhang mit der Doppelbrechung in Kristallen. Gelegentlich findet man aber auch "Fresnel zones and the corresponding Fresnel zone ellipsoids", z. B. in [Orfanidis 2016/18], Example 18.14.2 (S. 830) –. So sind wohl auch: "Fresnel-Zone", "-Parabel", "-Paraboloid", "-…" berechtigte Bezeichnungen.

Unter einer Fresnel-Zone wird jeweils der Bereich zwischen zwei zu ganzzahligen ν gehörenden, aufeinanderfolgenden Umweg-Ellipsen (Fresnel-Zonen-Ellipsen, verallgemeinert – siehe oben – Umweg-Ellipsoiden, Fresnel-Zonen-Ellipsoiden) verstanden, von denen sie begrenzt wird. Die Begrenzungsflächen und die Fresnelzonen selbst liegen somit konzentrisch (ähnlich dem Inneren einer Zwiebel) zur Sichtlinie (LOS), wie auch deren kreisförmige Schnittlinien mit einer zur Sichtlinie rechtwinkligen Schnittebene. Aus den geometrischen Gegebenheiten ergibt sich eine Übereinstimmung der Flächeninhalte aller mit der Entfernung von der Sichtlinie in immer engerem Abstand aufeinanderfolgenden Zonen.

Die Umwege benachbarter Fresnelzonen-Ellipsen unterscheiden sich definitionsgemäß jeweils um eine halbe Wellenlänge (λ / 2). Wegen der damit verbundenen Verzögerung besteht eine Gegenphasigkeit der Signale korrespondierender Lagen innerhalb benachbarter Zonen – die Phasenlagen unterscheiden sich um π bzw. 180 °.

Unter Freifeldgegebenheiten liegt bei sehr großen Entfernungen zum Sender innerhalb der Schnittfläche ein homogener Energiedurchsatz vor, sodass wegen der Flächengleichheit jede Fresnelzone den gleichen Beitrag zum Empfangssignal liefert. Aufgrund der Gegenphasigkeit heben die Beiträge aus benachbarten Fresnelzonen paarweise einander auf: Es verbleibt allein der Beitrag aus der ersten Fresnelzone, der innersten, einer Kreisfläche. Die Wahrscheinlichkeit, dass die Querschnittsfläche eines Hindernisses einen größeren Teil oder sogar den gesamten Querschnitt einer einzelnen Fresnelzone vollständig verdeckt, so dass die resultierende Empfangsenergie verschwindet, ist für die Kreisfläche der 1. Fresnelzone bedeutend größer als bei den kreisringförmigen Fresnelzonen höherer Ordnung.

Diese erhöhte Empfindlichkeit erklärt den weit verbreiteten Eindruck, die Signalübertragung erfolge allein in der ersten Fresnelzone. Andererseits hat sie in der Funkpraxis die besondere Rolle des Wertes ν = 1 zurfolge: Es gilt der Grundsatz, dass sich zur Vermeidung von Empfangsbeeinträchtigungen in der 1. Fresnelzone keine Hindernisse befinden sollen, die allein schon durch ihre abschattende Wirkung eine Abschwächung des innerhalb einer Fresnelzone empfangenen Signals verursachen würden – entsprechend ihrem Anteil an der Fläche der betroffenen Fresnelzone. In der 1. Fresnelzone geht dieser voll ein. Im Fall äußerer Fresnelzonen ist er geometrisch bedingt eher kleiner, und sobald benachbarte Zonen betroffen sind, kann es zu gegenseitiger Aufhebung dieses Einflusses kommen. Die Erfahrung hatte gezeigt, dass schmale Hindernisse toleriert werden dürfen, solange ihr Abstand zur Sichtlinie eine Grenze von 60 % des Radius der 1. Fresnelzone einhält.

Auf den Einfluss eines geometrisch einfachen Objekts von der Gestalt einer "Scharfen Kante" ist im Eintrag "Beugung der GPS-Signale an Kanten abschattender Hindernisse" eingegangen. Für Fresnelzonen-Betrachtungen interessiert der Fall mit Empfang oberhalb der Schattengrenze. Dabei entsprechen den Grenzen der n-ten Fresnel-Zonen ν_Fz = n betragsgleiche negativ-ganzzahlige ν_KNM = -n ("KNM": "KNife edge Model").

Größenvorstellungen zu den Ausmaßen der Fresnelzonen (nach Umrechnung auch für vom zivilen L2-GPS-Signal abweichende Frequenzen) können Bilder im Eintrag "Beugung der GPS-Signale an Kanten abschattender Hindernisse" und das obige Bild 4 vermitteln. Dort findet man z. B. für den Durchmesser der 1. Fresnelzone bei einem Abstand d = 50 m von der L-Band-Empfangsantenne d_F1 = 2 h_ν=1 = 6 m; bei den etwa sechsmal größeren Satelliten-TV-Frequenzen erhielte man nur noch 1 m. Vom Ort der Antenne als Blickpunkt aus entsprechen diesen beiden Werten sehr kleine Winkelablagen gegenüber der Sichtlinie: 2 ⋅ 3,4° für GPS- bzw. 2 ⋅ 0,5° für Sat-TV-Frequenzen. In dieser Größenordnung bewegen sich die 3-dB-Öffnungswinkel der Hauptempfangskeule von Richtantennen. (Außerhalb dieser Betrachtungsweise bleiben Beeinträchtigungen durch Umwegsignale, die an größeren reflektierenden Objekten entstehen und – falls die Absenkung allein durch die Richtwirkung nicht ausreicht – durch die Wahl eines geeigneten Aufstellorts der Antenne zu vermeiden sind).

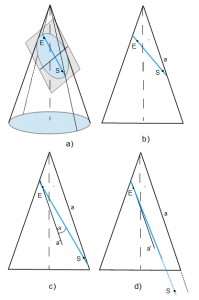^Anm3  – etwas grob ausgedrückt "eine Frage des Maßstabs";
Näheres unter Zuhilfenahme der nebenstehenden Darstellungen:

Im Bild a) ist eine Umweg-Ellipse dargestellt, als Schnittbild einer Ebene mit einem Kegel (nach unten beliebig lang), in den Brennpunkten der Sender S (unten) und der Empfänger E. Der (auf der Hauptachse der Ellipse gemessene) Abstand zwischen S oder E und dem jeweils benachbarten Scheitel entspricht einem bestimmten – verglichen mit dem Abstand zwischen Sender und Empfänger relativ großen – Umweg. Für die folgende Betrachtung ist die Darstellung des Kegels in der Seitenansicht besser geeignet – so in Bild b) für das Bild a).

Die weiteren Bilder kann man sich als in der Weise aus dem Bild b) entstanden vorstellen, dass der senderseitige Scheitel entlang der Mantellinie a unter Beibehaltung des an den beiden Scheiteln ablesbaren Umwegs abwärts verschoben ist. Dabei nimmt der Winkel α zwischen der Ellipsenebene und der zur besseren Veranschaulichung parallel zu a eingetragenen Linie a’ ab, bei der es sich ihrerseits um die Schnittlinie einer wie die Ellipsenebene senkrecht zur Papierebene ausgerichteten Ebene mit der Papierebene handelt.

Im Bild d) befindet sich schließlich S weit unterhalb der unteren Bildbegrenzung, was der Situation beim Satellitenempfang bereits näher kommt. Parallele Lage der Schnittebene (von Sender und Empfänger) mit der Kegel-Mantellinie ist aber das Kriterium dafür, dass mit der Schnittlinie eine Parabel vorliegt. Für einen gegebenen Punkt der (ursprünglich einer Ellipse entsprechenden) Schnittlinie ist die Annäherung an eine Parabel umso besser, je kleiner der kürzeste Abstand dieses Punktes von der a’-Ebene ist. Dabei wird ersichtlich, dass sich dieser Bereich mit größerer Entfernung des Empfängers vom Sender in Richtung zum Sender weitet.

^Anm4  Das trifft für alle einfallenden Parallelstrahlen zu, wenn die Reflexionen an einem Spiegel oder an Ausschnitten aus mehreren Spiegeln erfolgen, die selbst die Form einer Parabel haben (Beispiele: Parabolantenne – ein einziges Paraboloid; Ensemble von Ausschnitten aus vielen ν-Rotations-Paraboloiden, bei dem eine weitläufige Verwandtschaft mit den Fresnel-Kollektoren der Solartechnik besteht – nicht zu verwechseln mit der Spiegel-Anordnung, seit bereits viel längerer Zeit häufig ebenfalls einfach "Fresnel-Spiegel" genannt, des "Fresnelschen (oft richtiger "Doppel"-)Spiegelversuchs" – Näheres dazu z. B. in einem Beitrag in Wikipedia).
Zu beliebigen reflektierenden Objekten müssten aber eher unterschiedliche Parabelanordnungen zuzuordnen sein.

^Anm5  Im allgemeinen geht es um den Empfang einer Vielzahl von Satelliten.

Der Vorgehensweise zu beispielsweise den Strahlen I und II entspricht die Frage "Wohin gibt ein reflektierendes Objekt die Signale der einzelnen Satelliten weiter?"

Zur Betrachtung mit vom Emnpfänger ausgehendem Strahl könnte die Fragestellung in etwa lauten "Von welcher Stelle am Himmel aus, ggf. von welchem Satelliten, besteht über das spiegelnde Objekt eine Empfangsmöglichkeit?". Zu diesem Strahlenbild, nur mit entgegengesetzt gerichtetem Durchlauf, würde aber auch die Frage passen "Von wo aus kann man im Spiegel den Empfänger sehen?".

^Anm6  Der Winkel, den die geneigte Ebene und die senkrecht stehende Wand unterhalb der Ebene einschließen, wird umso spitzwinkliger je mehr die Ebene nach oben geneigt wird, so dass eine somit ebenfalls gegenüber der Wand geneigte Linie l kein Einfallslot mehr sein kann.

^Anm7  Ein idealer Aufstellort einer GPS-Empfangsantenne befindet sich unmittelbar am Boden einer weitläufigen horizontalen Ebene – vgl. die Empfangsbedingungen beim Test von iBlue747, WPL-2000 und PocketGPS S1/PG-S1 ("Tests zu den internen Beiträgen zum Positionierungs-Fehler …") in Klaus‘ GPS-Ecke.

^Anm8  In dieser ursprünglichen Form betrifft das Babinetsche Prinzip die Beugungseigenschaften komplementärer flächiger Objekte. Der Ansatz der Komplementarität ist ebenfalls im Babinetschen Prinzip der Funktechnik, speziell in der Antennentechnik, erstmals wohl bei [Booker 1946], zu finden. Die komplementären Objekte sind hier der Halbwellendipol und die Schlitzantenne (siehe auch [Wolff Radartutorial], [Rolke Antennen]). Unter Berücksichtigung einiger zueinander dualer Gegebenheiten (u. a. "Strom ⇔ Spannung", Lage der Einspeisepunkte) stimmen Antennencharakteristiken und -gewinne beider überein.

^Anm9  Beispiel: Die Wanddämpfung d_w betrage
d_w = 10 dB .
Dann wird der Beitrag des Fensters zum Signal im Rauminneren bei einer Wandfläche vom Zehnfachen der Fensterfläche erreicht.

^Anm10  Bei Objekten beliebiger Größe (oder zumindest ausreichender Größe, wie z. B. im Fall eines Empfängers über rauem Erdboden, also ohne die für diesen Eintrag vorgenommene Beschränkung auf räumlich begrenzte, d. h. kleine Objekte) sind ohnehin diese drei Arten der Signalweitergabe gleichzeitig anzutreffen – abhängig von der Orientierung der betrachteten Punkte des Objekts bezüglich Signalquelle und Empfänger; ein kleines Objekt entspricht einem begrenzten Ausschnitt daraus, wobei dann noch die Beugungseffekte an den begrenzenden Konturen zu berücksichtigen sind.

Verweise

[Gross 2003] Gross, R.: Lecture Notes of Prof. Gross to the Lectures "Physics 3" (WS 2001/2002 and WS 2002/2003), Kapitel 5 Beugung und Interferenz. Walther-Meissner-Institut Bayerische Akademie der Wissenschaften und Lehrstuhl für Technische Physik (E23) Technische Universität München, 2003 – Web-Link (PDF) https://www.wmi.badw.de/fileadmin/WMI/Lecturenotes/Physics_3/Gross_Physik_III_Kap_5.pdf

[Keydel 2010] Keydel, W.: Vorlesungsmanuskripte "1.5 Reflexion, Streuung und Eindringtiefe von EMW" – Friedrich-Alexander-Universität Erlangen-Nürnberg 2010 – Web-Link (PDF)

[Booker 1946] Booker, Henry G.: Slot aerials and their relation to complementary wire aerials (Babinet’s principle). Radiolocation, Journal of the Institution of Electrical Engineers – Part IIIA, 1946, 93. Jg., Nr. 4, S. 620-626, eingesehen hier am 14.05.2023

[Rolke Antennen] Web-Link (www.wolfgang-rolke.de/antennas)

[Wolff Radartutorial] Web-Link (www.radartutorial.eu)

[Orfanidis 2016/18] Orfanidis, J. S.: Electromagnetic Waves and Antennas, Kap. 18 Radiation from Apertures. Rutgers University, Piscataway, NJ (USA), August 2016 – Web-Link (PDF). https://www.ece.rutgers.edu/ – Dateidatum 22.07.2016)

[Michler, Strey 1998]  Michler, O.; Strey, M.: DAB-Indoor-Versorgung im L-Band – Ausbreitungsmessungen und Untersuchungen zur Verbesserung der DAB-Indoor-Versorgung. Schriftenreihe der SLM, Band 6, VISTAS-Verlag, Berlin, 1998 (ISBN 3-89158-222-6).

[Strang ua 2008] T. Strang, F. Schubert, S. Thölert, R. Oberweis, u. a.: Lokalisierungsverfahren. Deutsches Zentrum für Luft- und Raumfahrt (DLR), Wessling, 2008 – Web-Link (PDF)

[Lehner u.a. 2009] Lehner, A.; Steingass, A.; Schubert, F.: A Location and Movement Dependent GNSS Multipath Error Model for Pedestrian Applications. In: Proceedings European Navigation Conference. ENC-GNSS 2009, Neapel – vergleiche Web-Link (PDF) (Inhalt der Publikation zugänglich dank OpenAccess in der Helmholtz-Gemeinschaft – OpenAccess in der Helmholtz-Gemeinschaft)

Klaus Dannowski – Klaus‘ GPS-Ecke
O1.O5.2O13