Stand 05.08.2020

Ausbreitungshindernisse beim Satellitenempfang

Selbst bei großen Erhebungswinkeln der Satelliten über dem Horizont ragt oft (zeitlich und örtlich; die "Elevation" der Satelliten erreicht nur selten 90°) eine Vielzahl von Objekten, z. B. Bauwerke oder Berge, nach oben oder auch mehr seitlich in die Sicht-Linie Satellit – Empfänger hinein. Für den Empfänger verdecken sie so die Sicht zum Satellit. Dennoch breiten sich die GPS-Funkwellen von den Kanten (waagerechten, geneigten, senkrechten) der Hindernisse ausgehend aufgrund von

Beugung (Diffraktion)

in den gegenüber dem direkten Signal abgeschatteten Bereich aus, wo sie zusammen mit den aus Reflexionen stammenden Signalbeiträgen desselben Satelliten die Empfangsantenne erreichen – auf einem Weg, der wie bei diesen ebenfalls stets länger ist als die direkte (LOS-) Entfernung.

Auswirkung der kleinen Wellenlänge

Allerdings ist es eine Gegebenheit der kleinen Wellenlänge der GPS-L1-Frequenz (λ ≈ 19 cm), dass der Pegel der weitergegebenen Satellitensignale abhängig vom Überstand der Kante über der Verbindungslinie Satellit-Empfänger bereits bei Umwegen von maximal 1 m rasch abnimmt. So spielt bei üblichen mobil genutzten GPS-Geräten weniger der vergleichsweise kleine Umweg der gebeugten GPS-Signale der Satelliten eine Rolle als der Umstand, dass dieser Pegelverlust bei der auf der Beugung beruhenden Ausbreitung dazu führt, dass der Empfänger nur noch die im NLOS-Bereich mit weniger abgesenkten Pegeln, aber größeren Umwegen behafteten reflektierten Signalbeiträge erhält^Anm1).

Fresnel-Beugung und Fraunhofer-Beugung

Abhängig von der Entfernung des beugenden Objekts vom Empfänger einerseits und der Ausdehnung des Objekts andererseits wird dabei zwischen Fresnel-Beugung und Fraunhofer-Beugung unterschieden^Anm2). Für Betrachtungen zum GPS-Empfang können beugende Hindernisse in Entfernungen von einigen hundert Wellenlängen durchaus noch von Bedeutung sein. Diesem Bereich wird die Behandlung als Fraunhofer-Beugung gerecht.

Modell der "scharfen Kante" – "Knife-Edge"-Model

Praktisch vorkommende langgestreckte Hindernisse größerer Ausdehnung kann man sich idealisierend durch eine abschattende Halbebene ersetzt denken. Zur theoretischen Behandlung der Beugung, hier als Fresnel-Beugung, wird von einer rechteckigen Öffnung in einer im Vergleich zur Wellenlänge dünnen, für die Wellen undurchlässigen Platte ausgegangen mit der Signalquelle auf der einen und dem Empfänger auf der anderen Seite der Platte ([Gross 2003], [Orfanidis 2016/18]): Sämtliche (also in der Ebene der Platte gelegenen) Punkte der Öffnung sowie die Berandungen der Öffnung sind Ausgangspunkt von Elementarwellen. Die Signalintensität am jeweiligen Ort des Empfängers ergibt sich aus der Summation nach Betrag und Phase ("phasen- und betragsbewertete" Summation – entspricht "Überlagerung", "Interferenz") aller dort eintreffenden Elementarwellen mit von den jeweils durchlaufenen Strecken bestimmten Beträgen und Phasenlagen. Das Verhalten an der abschattenden Halbebene erhält man anschaulich, wie auch in der mathematischen Herleitung, durch Grenzübergang von Breite und Höhe der rechteckigen Öffnung gegen ∞: Aus dem Rechteck wird eine "scharfe Kante", engl. "knife-edge", "straight-edge" diffraction.

In [Gross 2003], Seiten 215, 216, wird – bezogen auf die langgestreckte und geradlinige Kante ("Scharfe Kante", Fall der abschattenden "Halbebene") – angemerkt, dass von der Kante ein Intensitätsverlauf ausgeht, der nicht nur im Schatten- sondern auch im hellen Bereich dem einer "divergierenden, zylindersymmetrischen Kantenwelle" entspricht, die von einer Linienquelle im Bereich der Kante stammt^Anm3).

Berechnung der Beugungs-Dämpfung – Beugungsparameter ν

Bei [Gross 2003] mündet die Herleitung zur aufgrund der Beugung am Empfänger zu erwartenden Intensität in der grafischen Veranschaulichung (Seiten 214 - 215: Cornu-Spirale). In [Orfanidis 2016/18], S. 827 – 829, resultiert die allgemeine mathematische Herleitung bei Zahlenwerten in einer zugeschnittenen Formel für die Beugungsdämpfung (Gl. 18.14.9), zu der als Bezug auf (Gl. 31) – ebenfalls für die Beugungsdämpfung – in der für Ausbreitungs-Berechnungen bzw. -Prognosen eigentlich terrestrischer Funkverbindungen vorgesehenen ITU-Empfehlung [ITU_526-14], Seite 19, verwiesen ist.

Allein den Pegelunterschied Δ p gegenüber dem LOS-Anteil (auch als Kantenbeugungsdämpfung a‍ ‍_b angegeben) bestimmender Parameter ist demnach

der durch das Hineinragen der Kante in den Übertragungsweg gegebene Beugungsparameter ν (griech. Buchstabe "nü", "ny"). Bei ihm handelt es sich um den auf die halbe Wellenlänge bezogenen Umweg u, um den der vom Sender zum Empfänger verlaufende Weg (also die Summe der jeweils geradlinig zwischen Sender bzw. Empfänger und Kante gemessenen Verbindungslinien) länger ist als die Verbindung entlang der (ggf. verdeckten) Sichtlinie zwischen beiden – also

ν = ‍u ‍/‍ ‍(λ/2).

Im Fall des Satellitenempfangs entsteht ein relevanter Wegunterschied allein zwischen Kante und Empfangsantenne.

Oberflächlich betrachtet unterscheiden sich Gl. 18.14.8 (Orfanidis) und Gl. 31 (ITU). Der Grund ist die unterschiedliche Vorzeichenwahl von ν – in [ITU_526-14] wie in der GPS-Literatur überwiegend gebräuchlich:

• Kante unterhalb Schattengrenze (LOS-Empfang): ν < 0 ,
• Kante an Schattengrenze: ν = 0 ,
• Kante oberhalb LOS (Empfang im abgeschatteten Bereich): ν > 0 .

Das Vorzeichen in [Orfanidis 2016/18] ist entgegengesetzt dazu^Anm4):

ν‍ ‍= ‍ν‍ ‍_ITU=‍ ‍–ν‍ ‍_Orfani‍ ‍ .

Sind die Kanten üblicher Hindernisse im Unterschied zur idealisierenden scharfen Kante (Rundungsradius in der Größenordnung eines Teils einer Wellenlänge) abgerundet (Rundungsradius in der Größenordnung einzelner Wellenlängen), so kommt es in diesem Kantenbereich bei ν > 0 selbst wiederum zur Abschattung der an der Original-Schattengrenze entstandenen gebeugten Elementarwellen. Das wird mit einem vom Rundungsradius abhängigen Zuschlag zur Beugungsdämpfung der scharfen Kante berücksichtigt (siehe z. B. [ITU_526-14], S. 19). So ist erstrecht davon auszugehen, dass die Pegel gebeugter Funk-Signale im abgeschatteten Gebiet fast immer von denen der Beiträge aus Reflexionen übertroffen werden. Dagegen ist im LOS-Fall (ν < 0) als Effekt eines endlichen Rundungsradius die Entstehung zusätzlicher Elementarwellen (wenn nicht sogar das Zustandekommen von Reflexion) an der Kantenrundung mit der Folge eines Pegelzuwachses, wegen der innerhalb der Rundung veränderlichen Entstehungsorte aber auch stärker ausgeprägten Pegeländerungen über ν denkbar.

Der Beugungsparameter ν beim Satellitenempfang

Neben weiteren ebenfalls aus der Theorie hervorgegangenen Ansätzen zur zahlenmäßigen Abschätzung einer Vielzahl terrestrischer Ausbreitungssituationen enthält die ITU-Empfehlung [ITU_526-14] auf den Seiten 16 und 17 mehrere Bilder und Berechnungsformeln für den Beugungsparameter ν.

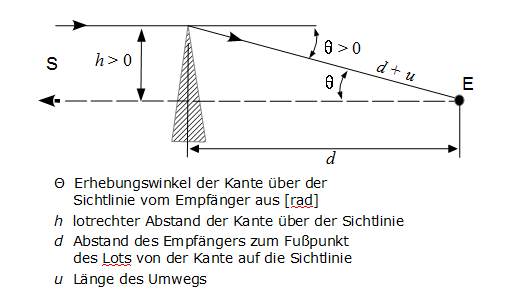
Bild 1: Umweg u beim Satellitenempfang
über eine scharfe Kante

Der Situation beim Satellitenempfang kommt das Bild 8a) auf Seite 17 am nächsten. Es lässt sich leicht an die Gegebenheiten des Satellitensenders anpassen – siehe Bild 1 (rechts): Aufgrund der sehr großen Entfernung zur Satellitenantenne wird dort die Teilstrecke "Sender – Kante", d₁, sehr groß und geht somit in eine Parallele zur gegebenenfalls verdeckten Sichtlinie über (Wellenfronten eben)^Anm5). Dabei geht somit im oben genannten Bild 8a α₁ gegen 0, und zugleich werden α₂ und Θ einander gleich. Abhängig von der Elevation des Satelliten und der Ausrichtung der Kante ist die Darstellung lediglich noch durch Neigen der Darstellung auf den Satelliten auszurichten und ggf. zwecks Anpassung an eine
   gegenüber der Horizontebene geneigte Kante
um die Sichtlinie zu rotieren.

Mit dieser Ausrichtung findet sich der Umweg allein bei der Verbindung "Kante – Empfänger" als u im rechtwinkligen Dreieck rechts mit den Seiten

"Lot von der Kante auf die Sichtlinie"
"Verbindung E mit dem Fußpunkt dieses Lots"
"Verbindung E mit der Kante".

Der Betrag des Beugungsparameters ν (siehe obige Definition) berechnet sich daraus gemäß

ν =u/(λ/2) .

Ergebnis einer einfachen Herleitung sind die Berechnungsformeln für ν (Bezeichnungen siehe Bild 1)

– abhängig von h:

– abhängig von Θ:

Beispiele für Zahlenwerte des Betrags von ν, Satellitenfrequenz f = 1575 MHz, sind den beiden folgenden Diagrammen zu entnehmen (zum Vorzeichen siehe oben).

Bild 2: Verlauf des Beugungsparameters ν abhängig vom Überstand h

Bild 3: Verlauf des Beugungsparameters ν abhängig vom Erhebungswinkel Θ der Kante über der Sichtlinie

Mit dem gefundenen ν-Wert wird dann die Kantenbeugungsdämpfung a_b bestimmt. Eine Formel für den abgeschatteten Bereich und ein Diagramm finden sich in [ITU_526-14], Seite 18, als Gl. (31) bzw. Figure 9 oder in [Orfanidis 2016/18], Seite 829 (Gl. 18.14.8) bzw. Fig. 18.14.2 ebenfalls auf Seite 829.

Bemerkenswerte Einzelheiten der Beugungsdämpfung:

• Bereits bei |ν| = 2 – entspricht einem Umweg von nur erst 19 cm – wird im abgeschatteten Bereich a_b = 20 dB erreicht.
• Die von der Kante ausgehenden Elementarwellen erreichen auch eine Empfangsantenne, die sich noch im LOS-Gebiet befindet. Letztlich ist es wohl deren Interferenz mit den Wellen des LOS-Signals, die den abhängig von ν um den LOS-Wert pendelnden Pegelverlauf verursacht.
• Bei ν = 0 bewirkt die Interferenz aus LOS-Signal und Kanten-Signal zusammen mit der einsetzenden Abschattung eine Absenkung der Intensität des resultierenden Signals (z. B. die Empfangsspannung) gegenüber der des LoS-Signals auf die Hälfte entsprechend einer Pegelabsenkung um 6 dB^Anm6).

Bild 4 – Beugung beim Satellitenempfang: Verlauf des Überstands h der Kante über deren Abstand d zur Empfangsantenne

Eine interessante Fragestellung ist noch die nach der Höhe bzw. dem Überstand  h der Kante über der Sichtlinie bei vorgegebenem Betrag des Beugungsparameters ν. Sie gehorcht der Gl. 3 der obigen einfachen Herleitung: Bei den Verläufen im Plot von Bild 4 handelt es sich somit um die Äste von Parabeln, deren Scheitel bei d0 = – ν·λ/4 <  Klick für größeres Bild liegen. Aus dem Parabelverlauf ergibt sich, dass h schwächer als linear mit dem Abstand von der Empfangsantenne wächst.

Unter einem Vorbehalt kann an der zur Position (d‍,‍h) der Kante gehörenden Parabel der Wert von ν abgelesen werden.

Der Vorbehalt:

• Im durch das Hindernis abgeschatteten Bereich ("Kante oberhalb der Schattengrenze [≡ LOS/Sichtlinie entlang der Kante]"; 1. Quadrant des Diagramms) ist auf die abgelesenen ν-Werte das positive Vorzeichen anzuwenden.
• Im Bereich mit LOS-Beteiligung ("Kante unterhalb der Schattengrenze"; 4. Quadrant des Diagramms) ist auf die abgelesenen ν-Werte – wie dort bereits angetragen – das negative Vorzeichen anzuwenden.

Grafische Veranschaulichung: Ein Beispiel

Interessanter als allein die Darstellung von Rechenergebnissen für ν erscheint allerdings die folgende geometrisch anschauliche Interpretation von Bild 4.

Sie besteht darin, gedanklich die d,h-Ebene so zu orientieren, dass die beugende Kante zu einem Lot auf sie wird (die Bickrichtung auf das Bild liegt nun parallel zur Kante), und die Abszissenachse mit der – falls erforderlich auch durch das Kantenobjekt hindurch fortgesetzt zu denkenden – Sichtlinie zur Deckung zu bringen. Im Koordinatenursprung wird der Empfänger angenommen, wobei nun – maßstäbliche Anpassung vorausgesetzt – d und h die Positionen der Kante bzw. deren Lot auf die Sichtlinie angeben. Dieses Vorgehen soll mit dem Bild 5 verdeutlicht werden (Teilung beider Achsen in Metern^Anm7)).

Dabei hat man sich den Satellit "rechts vom Empfänger" vorzustellen und die Abszissenachse (zugleich die Sichtlinie, LOS, und die "Parabel" für ν = 0) zusammen mit den Parabeln zum Satelliten ausgerichtet, also um eine parallel zur Kante verlaufende Achse aufwärts geneigt, zu denken. Beim Neigen verringert sich in der obigen Darstellung zur Definition des Umwegs (in Bild 1) der lotrechte Abstand h entsprechend dem Cosinus des Elevationswinkels des Satelliten, nimmt also mit dessen Anhebung über den Horizont ab, bis die Kante die Sichtlinie frei gibt oder auch von ihr überragt wird (dann mit negativem Vorzeichen entsprechend den unteren Parabelästen). Von der Horizontalen abweichende Kanten können durch Rotieren der Darstellung um die LOS-Linie Berücksichtigung finden^Anm8).

Weiter von Interesse ist der Verlauf jenseits des streifenden Vorbeigangs der Sichtlinie an der Kante (mit ν = 0), d. h. bei Werten ν < 0. Hier beläuft sich die Wegstrecke für ν = 0 bis ν = -2 auf 6,5 m. Innerhalb dieser würde sich bei dem idealisierenden Knife-Edge-Modell die Beugungsdämpfung von 6 dB auf ca. 20 dB ändern.

Anhand von Bild 5 ist leicht die Abhängigkeit der jeweiligen Wegstrecken von der Elevation des Satelliten für ein bestimmtes beugendes Hindernis zu erkennen: Mit größerer Elevation werden die Strecken kürzer, wobei aber geometrisch bedingte Grenzwerte wirksam sind. Für die Strecke des obigen ν-Bereichs beläuft sich der Grenzwert auf ca. 6,5 m. Zu ihm gehört eine Elevation von ca. 80°. Weil sich dabei die Antenne bereits lotrecht unter der Kante befindet, ist für diesen Kantenüberstand (15 m gegenüber der Antenne) bei noch größerer Elevation eine Abschattung stärker als auf ν = -2 nicht mehr erreichbar.

Grenzen des Knife-Edge-Modells

Reale Empfangsumgebungen, die dieser einfachen Situation des Knife-Edge-Modells entsprechen, sind allergings nur selten anzutreffen sondern gehören eher zu den Ausnahmen. Das gilt u. a. für die als sehr groß vorausgesetzte Länge der Kante. Naheliegend ist hier die Vorstellung, dass sich die kurze Kante, anders als die ideal lange Kante innerhalb einer gegenüber dieser begrenzten, sogar eher kleinen Anzahl von Fresnelzonen erstreckt, die sich dann zudem abhängig von der Position der Empfangsantenne bezüglich der Kante ändert. Besonders im LOS-Fall könnte eine Auswirkung der kleinen Anzahl eine – verglichen mit dem idealen Knife-Edge-Modell – Vergrößerung der Pendelungen des Empfangspegels über ν sein. Hinzukommen Beiträge sich regelmäßig an den Enden kurzer horizontaler Kanten anschließender vertikaler oder geneigter Kanten.

Ebenfalls selten wird die Ausrichtung der Kante orthogonal zur Sichtlinie zutreffen.

Aufgrund der Erhebung der Satelliten (Elevation) werden zudem sowohl umliegende Objekte als auch der Boden von an anderen Objekten gebeugten Wellen getroffen. Das bedeutet deren mehr oder weniger kontinuierliche Ausleuchtung mit gebeugten, dabei unterschiedlich verzögerten Wellen des GPS-Signals, die wiederum infolge Spiegelung bzw. Streuung an die Empfangsantenne gelangen können^Anm9).

Eine weitere Auffälligkeit zeigt sich im Zusammenhang mit der Veränderung der Distanz zwischen den Positionen gegebener ν-Werte. Wie oben mit Verweis auf z. B. [Gross 2003], Seiten 215, 216 erwähnt, hat man davon auszugehen, dass den von beugenden geradlinigen Kanten ausgehenden Sekundärwellen, die einerseits (Empfang oberhalb der Kante) mit den direkt zur Antenne gelangenden Wellen interferieren, andererseits in den abgeschatteten Bereich strahlen, die Gestalt von Zylinderwellen zugrundeliegt. Die für sie charakteristische mit dem Radius bzw. den Abständen, Distanzen, zunehmende Dämpfung, aufgrund deren sich beispielsweise die Welligkeit des Empfangspegels oberhalt der Abschattungsgrenze veringern würde, tritt im Knife-Edge-Modell nicht in Erscheinung: Einzige Variable ist der Beugungsparameter ν.

Messbeispiel für die Beugungsdämpfung

Die Praxistauglichkeit einer gefundenen mathematischen Lösung ergibt sich aus dem Vergleich mit gemessenen Verläufen. Für den Fall der L-Band-Frequenzen der GPS-Signale würden geeignete Testaufbauten zur Beschaffenheit der Kantenbeugung, z. B. mit leitenden Platten in einer reflexionsarmen Umgebung, einen erheblichen Aufwand bedingen. Allerdings dürften wohl kaum jemals Zweifel bestanden haben, dass an entsprechenden für höhere Funkfrequenzen ausgelegten, weniger unhandlichen Testaufbauten zum Verlauf der Kanten-Beugungsdämpfung gewonnene Resultate prinzipiell auf L-Bandfrequenzen übertragen werden dürfen.

Um so interessanter ist die aus der Mehrwegkanal-Messkampagne des DLR von 2002 stammende Fig. 2 in [Lehner u.a. 2009]. Mit ihr liegt die Gegenüberstellung eines an einer Gebäudekante bei großem Dynamikbereich der Messung gewonnenen Verlaufs mit dem nach dem Knife-Edge-Modell berechneten Verlauf vor. Trotz einiger Auffälligkeiten darf sie – ganz besonders hinsichtlich des Verlaufs beim Empfang mit abgeschattetem Satellit – als Bestätigung des Knife-Edge-Modells gelten. "Auffälligkeiten": Es ist zu vermuten, dass mehrere störende Einflüsse am Messergebnis beteiligt sind. Zu diesen Einflüssen gehört, dass ein Hindernis in Gestalt einer Gebäudefront im Unterschied zur idealisierenden scharfen Kante eine sehr begrenzte Längsausdehnung aufweist, mit verschiedenartigen Auswirkungen, u. a. indem sich an den Gebäudeenden in anderer Richtung verlaufende Kanten anschließen, allerdings eher mit größerem ν-Wert, somit kleinerem Pegel. Hinzukommt, dass die eigentliche Form der Kante von der scharfen Kante abweicht, so dass es denkbar ist, dass es in Zusammenhang mit der Reflexion des direkten Satellitensignals im vom Empfänger abgewandten Kantenbereich zur Entstehung zusätzlicher Elementarwellen kommt, die zum eigentlichen gebeugten direkten Signalbeitrag als weitere, mit (aufgrund der Nähe zur Kante) nur geringfügig vergrößertem Umweg behaftete Umwegkomponente hinzutreten. Die Pendelungen des Empfangspegels vor der Schattengrenze sind intensiver als nach dem Knife-Edge-Modell zu erwarten wäre; der Pegel an der Schattengrenze (3386 m) gleicht etwa dem LOS-Pegel und liegt damit 6 dB über dem Knife-Edge-Verlauf. Als ein Hinweis auf die Beteiligung weiterer, allerdings bereits stärker abgesenkter Umweganteile mit vom stärkeren Signalbeitrag abweichendem Umweg könnten die wellenförmigen Verformungen bzw. "Kräuselungen" im Pegelverlauf ab etwa der Schattengrenze, aber auch im LOS-Bereich, gewertet werden^Anm10). Ähnliche Verformungen des Verlaufs wären jedoch auch zu erwarten, wenn die Fortbewegung mit ungleichförmiger Geschwindigkeit oder mit Schwankungen der Antenne oder nicht streng geradlinig – im Fall eines Fußgängers oft mehr oder weniger ausgeprägt – erfolgte.

Zusammenfassend

ist festzustellen: Für Alltagsanwendungen von GPS (wie auch jeglichem GNSS) mit unvermeidbarem großem Anteil reflektierter Signalbeiträge, also beim Navigieren oder beim Aufzeichnen von Tracks, ist der Einfluss von Beugungseffekten wegen der bereits bei noch kleinen Umwegen rasch zunehmenden Signaldämpfung zwar interessant, bleibt aber ohne praktische Auswirkung auf das Positionierungs-Ergebnis. Anders bei Präzisions-Anwendungen: Bei ihnen wird bereits bei der Aufstellung für Reflexionsarmut gesorgt. Dagegen kann der Pegel von Umweganteilen, die durch Beugung an der Berandung der Gerätegrundplatte aus im näheren Bereich unterhalb der Platte reflektierten Wellen entstehen, Werte erreichen, denen mit zusätzlichen Maßnahmen zur direkten Abschwächung oder mit Kompensation im Sinn allerdings aufwändiger Kalbibrierverfahren begegnet werden muss.

Anmerkungen

^Anm1  Anders bei Präzisionsanwendungen, bei denen es um Fehler im mm-Bereich geht: Oft ist es nicht vermeidbar, die GPS-Empfangsantenne in einigem Abstand über der Umgebung unterzubringen (im Beispiel "Parallelfahrsystem" in der Landwirtschaft am Traktor). Dabei wird die Antenne für Boden-Reflexionen erreichbar, mit – bezogen auf die Genauigkeitsforderung – gegebenenfalls sehr großen Umwegen und daher beträchtlicher Auswirkung und trotz von Hindernissen freiem Umfeld nicht akzeptablen Fehlern. Eine übliche Gegenmaßnahme gegen Signalbeiträge aus dem Raum unterhalb der Antenne ist, unter der Antenne eine leitende Grundplatte anzubringen (vorzugsweise kreisförmig, Durchmesser in der Größenordnung der Wellenlänge). Das allein sorgt noch nicht für die benötigte Unterdrückung des Einflusses der Bodenreflexionen, denn die vom Boden aus an die Grundplatte gelangenden Wellen werden um deren Berandung herum gebeugt, sodass sie die Empfangsantenne mit dennoch störender Intensität erreichen. Die benötigte Verbesserung wird (u. a. beispielsweise im Geospector GPS-Forum – vormals "kowoma GPS-Forum" – diskutiert oder auch auf Seite 2 eines Beitrags von NovAtel zur NovAtel GPS Pinwheel Antenna /Link gefunden bei OptimalSystem.DE.de/) erst erzielt, indem die Grundplatte zusätzlich strukturiert wird, beispielsweise indem auf der Platte konzentrisch zur Antenne Schutz-Ringe (Choke rings) angebracht werden. Das Optimum ihrer Bauhöhe – in der Nähe von λ/4 (siehe diesen Variantenvergleich sowie eine Tabelle mit Zahlenwerten bei UNAVCO.org ) – lässt eine Wirkungsweise in der Art der aus der Funktechnik bekannten λ/4-Stichleitungen bzw. -Sperrtöpfe, hier konzentrisch angeordnet, vermuten: Die an der Berandung der Grundplatte gebeugten Wellen lösen ihrerseits ebenso auch am oberen Rand der Ringe Sekundärwellen aus. Diese gelangen innerhalb der Ringe zu deren Grundplatte, von wo aus sie nach Reflexion wieder den Rand erreichen. Aufgrund der Wegstrecke von zweimal λ/4 sind sie dann aber gegenphasig zu den sie auslösenden gebeugten Wellen, so dass es zur gegenseitigen Abschwächung der an den nächst engeren Ring weitergegebenen auslösenden mit der am Boden des Rings reflektierten Welle kommt. Die Choke-Ringe behindern somit das Voranschreiten der um den Plattenrand gebeugten Wellen zur Antenne.

^Anm2  Abhängig von der Entfernung des Empfängers vom beugenden Objekt wird bei der theoretischen Behandlung zwischen dem (vgl. z. B. [Gross 2003], S. 201)

• Nahbereich – Bereich der "Fresnel-Beugung",
  die am Empfänger eintreffenden, vom Objekt ausgehenden Wellenfronten sind gekrümmt,

und dem

• Fernbereich – Bereich der "Fraunhofer-Beugung",
  die beteiligten Wellenfronten (sowohl die vom Objekt ausgehenden als auch – im Fall von Satellitensignalen stets erfüllt – die zum Objekt gelangenden) sind eben,

unterschieden.

Zahlenmäßige Bereichszuordnung (s. [Gross 2003], S. 202):

Dabei sind

ρ der Radius des Kreises, der die gesamte für den Empfänger wirksame Berandung des das Satellitensignal weitergebenden Objekts einschließt,

λ die Wellenlänge,

d der Abstand des Objekts von der Empfangsantenne.

Die beiden folgenden Bilder mögen das für den Fall der GPS-Signale (f = 1575 MHz) veranschaulichen.

Fraunhofer-Beugung (Fernbereich) und Fresnel-Beugung (Nahbereich):

Sowohl Gl. (5.2.15) für den Bereich der Fresnel-Beugung als auch Gl. (5.2.16) für den Bereich der Fraunhofer-Beugung lassen hohe Anforderungen sowohl an den Zylinder-/Kugel-Charakter der Wellen einerseits als auch an die Ebenheit der Wellenfronten andererseits erkennen.

^Anm3  Bei einem beliebig geformten Hindernis werden die Austritte der von ihm ausgehenden Elementarwellen dessen Schattenlinie bzw. -grenze folgen.

Für eine Veranschaulichung der Signalausbreitung durch Beugung an Kanten bietet sich das folgende Experiment an (in gedruckter Form so wohl erstmalig von Francesco Maria Grimaldi /1618 – 1663; Italien/ zusammen mit dem Begriff „Diffraction“ /lat.: Beugung; siehe [Grimaldi 1665], Seite 11/ für eine von ihm ausführlich untersuchte Ausbreitungsform von Licht beschrieben). Es besteht im visuellen Beobachten der Kante eines dünnen für Licht undurchlässigen Gegenstands (Messerschneide, Rasierklinge, Metallfolie; scharfkantig, dünn, genauer: mit sehr kleinem Krümmungsradius der Kante, um Reflexionen in deren Bereich auszuschließen) vor einem dunklen Hintergrund im Gegenlicht z. B. einer Taschenlampe durch eine Lupe. Schon mit geringfügiger Vergrößerung ist eine der Kante folgende linienförmige Aufhellung zu erkennen – sowohl, wenn dabei die Lichtquelle von dem Gegenstand verdeckt wird als auch, wenn sich die Lichtquelle oberhalb der Kante befindet. Im Fall eines Funksignals entspricht der kantennahe Lichtsaum dem Bereich, aus dem das Funksignal sowohl entsprechend seiner ursprünglichen Richtung an der Kante vorbei, als auch in den Schattenbereich hinter der Kante (bei ebenfalls vergleichbarer Richtungsabhängigkeit der Intensität) weitergegeben wird.

Umfangreiche Untersuchungen zur Beugung an der scharfen Kante, speziell von Licht, mit der Erwähnung von "Grimaldis leuchtender Kante" als Ausgangspunkt finden sich bei www.gebeugtes-licht.de, z. B. in der Arbeit [Nieke 1997] (in dieser u. a. mit fotografischen Großaufnahmen dokumentiert) bzw. in [Nieke 1997p].

^Anm4  "In sich", d. h. bei alleiniger Betrachtung der Beugungsdämpfung, ist diese Zuordnung durchaus anschaulich und damit sinnvoll: "ν größer" ergibt "Beugungsdämpfung größer". (Dabei ist zu bedenken, dass der Zusammenhang der ganzzahlig-positiven Nummern ν der Fresnel-Zonen mit dem Beugungsparameter ohnehin lediglich dessen Betrag ν betrifft.)

^Anm5  Enge Verwandschaft des Funkstrahl-Verlaufs bei Beugung mit dem bei Reflexion: Der Verlauf des Funkstrahls in diesem Bild könnte eben so zu einem am Ort der eigentlichen Beugungskante (oberes Ende der scharfen Kante) befindlichen Reflexionspunkt gehören – Ausgangspunkt beider Betrachtungen ist der Umweg gegenüber der Sichtlinie.

^Anm6  Gelegentlich wird diese ausgeprägte Pegelabsenkung dahingehend interpretiert, dass die Übertragung der Signalenergie vom Sender zum Empfänger innerhalb eines engen konzentrisch die Sichtlinie umgebenden Bereichs mit den Abmessungen der ersten Fresnelzone in der Art eines direkten, gerichteten Strahls stattfindet.

ν = 0 entspricht dem streifenden Vorbeigang der Sichtlinie an der Kante, so dass das Hindernis den Querschnitt der 1. Fresnelzone gerade zur Hälfte verdeckt. Sofort fällt als Widerspruch auf, dass die Pegelabsenkung um 6 dB eine Halbierung der Intensität (z. B. der Feldstärke), energetisch aber die Verringerung auf nur noch ein Viertel des Betrags ohne Hindernis bedeutet.

Wenn auch auf den Fall der Beugung eingeschränkt, lässt sich die Rolle der Fresnel-Zonen (z. B. [Gross 2003], ab S. 205) an der Wirkungsweise der Fresnelschen Zonenplatte erkennen (beschrieben u. a. in [Gross 2003], ab Seite 208 – Ausführungen zur Abbildung 5.9 von S. 210; für weitere Aspekte siehe auch Wikipedia(en)-Link): Aus der Fläche jeder ungeraden Zone (durch die Konstruktion erreicht – Lage und Breite der Ringe entsprechen dabei dem Schnittbild einer Ebene mit den Fresnel-Zonen-Ellipsoiden; die undurchlässigen Ringe der Platte verdecken die geradzahligen Zonen) entnimmt die Zonenplatte der (homogenen) ebenen Wellenfront die gleiche Energie wie aus der ersten und lenkt sie in den Brennpunkt der Platte (identisch mit dem Brennpunkt der Fresnel-Zonen-Ellipsoide). Andererseits würden sich im Brennpunkt mit der Empfangsantenne aufgrund von Interferenzen die Beiträge benachbarter Zonen (wie auch jeder anderen ungeradzahlig abweichenden Zone) sogar zu Null aufheben.

Tatsächlich ist der Beitrag zum Gesamt-Empfangspegel aus den Fresnelzonen höherer Ordnung energetisch gesehen oft relativ klein, denn wegen des mit der Ordnung wachsenden Durchmessers einer Fresnelzone sinkt die Wahrscheinlichkeit, dass in einer Empfängerumgebung in diesen Zonen befindliche Objekte jeweils einen wesentlichen Teil der für alle Zonen betragsgleichen Querschnittsfläche einer einzelnen Zone einnehmen.

Mit diesen Betrachtungen soll verdeutlicht werden, dass der bei der Beurteilung der Geometrie von Funkübertragungsstrecken hilfreiche "Fresnelzonen-Ansatz" nicht für die Beschreibung der Energieverteilung in einer Empfängerumgebung in der gelegentlich anzutreffenden oben angedeuteten Art geeignet ist.

^Anm7  In diesem Bild wurden für die Achsenteilungen übereinstimmende Maßstäbe gewählt. Anders als im Bild 4 zeigt sich so der sehr schlanke Verlauf der ν-Parabeln, der aus der großen Senderentfernung folgt.

^Anm8  Unter Berücksichtigung beliebig zur Horizontebene orientierter Kanten werden aus den Parabelästen Rotations-Paraboloide, wegen des Vorzeichens bei ν genauer wohl Rotations-Halb-Paraboloide.

^Anm9  1. "kontinuierlich": Bei den ν-Linien des Diagramms handelt es sich ja nur um eine als Orientierung gedachte Auswahl aus der Schar der beliebig eng liegenden Parabeln (ν ist eine reelle Zahl).
2. Mögliche Folge: Reflexion auch der gebeugten Wellen an Objekten der Umgebung oder am Boden, spiegelnd wie auch diffus, mit der Auswirkung, dass die Empfangsantenne von diffus reflektierten gebeugten Wellen auch kleinerer ν (neben ebenfalls diffus, aber in größerer Entfernung reflektierten direkt zum Boden gelangten Wellen) ein und desselben Satellits getroffen werden kann.

^Anm10  Ergänzung Juli 2014 / Juni 2015
Eine Bestätigung dieser Vermutung zum Pegel-Verlauf in der hier betrachteten Fig. 2 liefern die Ergebnisse einer Modellanalyse in [Lehner, Steingass 2014] (mit der leicht modifizierten Fig. 16 – Link). In der Empfangsumgebung gemäß Fig. 23 ist es offensichtlich der Satellit No. 1, dessen LOS-Pfad die ca. 15 m hoch gelegene Oberkante einer Gebäudefront streifend passiert. Hierfür erscheinen im Analyseergebnis – Fig. 24, Satellite 1 (30°;-45°) – zwei nur geringfügig gegeneinander verzögerte, um ca. 23 dB unterschiedliche Signalbeiträge.

Verweise

[Gross 2003] Gross, R.: Lecture Notes of Prof. Gross to the Lectures "Physics 3″ (WS 2001/2002 and WS 2002/2003), Kapitel 5 Beugung und Interferenz. Walther-Meissner-Institut Bayerische Akademie der Wissenschaften und Lehrstuhl für Technische Physik (E23) Technische Universität München, 2003 – Web-Link (PDF) (07.07.2021: nur Auszüge – war https://www.wmi.badw.de/fileadmin/WMI/Lecturenotes/Physics_3/Gross_Physik_III_Kap_5.pdf

[ITU_526-14] Recommendation ITU-R P.526-14 (01/2018) – Propagation by diffraction (Fassung in Englisch). International Telecommunication Union (ITU), Genf, 2018 – Web-Link (PDF) (https://www.itu.int/rec/R-REC-P.526-14-201801-I/en)

[Orfanidis 2016/18] Orfanidis, J. S.: Electromagnetic Waves and Antennas, Kap. 17 Radiation from Apertures. Rutgers University, Piscataway, NJ (USA), August 2016 – Web-Link (PDF). (http://snf-829109.vm.okeanos.grnet.gr/files/Ebooks/Electromagnetic%20Waves%20and%20Antennas%20S%20Orfanidis/ch17.pdf – Dateidatum 22.07.2016)

[Grimaldi 1665] Grimaldi, F. M.: Physico-mathesis de lumine, coloribus, et iride (in Latein). Vittorio Bonati, Bologna ("Bononiae"), Italien, 1665. Web-Link (Google Books)

[Nieke 1997] Nieke, H.: Newtons Beugungsexperimente und ihre Weiterführung – Arbeit 01 "Die Newtonschen und Fresnelschen Beugungsexperimente" (1997 / Dateidatum 2007). Web-Link (PDF)

[Nieke 1997p] Nieke, H.: Newtons Beugungsexperimente und ihre historischen und philosophischen Folgerungen. Halle (Saale), Germany : H. Nieke, 1997 – Web-Link (PDF)

[Lehner u.a. 2009] Lehner, A.; Steingass, A.; Schubert, F.: A Location and Movement Dependent GNSS Multipath Error Model for Pedestrian Applications. In: Proceedings European Navigation Conference. ENC-GNSS 2009, Neapel – vergleiche Web-Link (PDF) (Inhalt der Publikation zugänglich dank OpenAccess in der Helmholtz-Gemeinschaft – OpenAccess in der Helmholtz-Gemeinschaft)

[Lehner, Steingass 2014] Lehner, A.; Steingaß, A.: Spatial Dynamic Wideband Modeling of the MIMO Satellite-to-Earth Channel. International Journal of Antennas and Propagation Volume 2014; Article ID 102754; Hindawi Publishing Corporation, Kairo 2014 – PDF-Download 1 (Hindawi – Creative Commons Attribution License) / PDF-Download 2 (DLR – Open access Article – Copyright © 2014 A. Lehner and A. Steingaß)

Klaus Dannowski – Klaus‘ GPS-Ecke
O1.12.2O11

"Diffraction of the signals transmitted by GPS satellites at edges of shadowing obstacles"